Dr.Hab., Professor Y.P. Kobyakov¹
Postgraduate, Honorary Master of Sports A.V. Lovchev^1
1Vladimir State University named after A.G. and N.G. Stoletovs, Vladimir

Keywords: training process, training workload, rating, SI systemю

Background. At every stage of a training system from the process design to the competitive progress rating and analyzing, sport experts widely apply the process scope and intensity rating values for their analyses. L.P. Matveyev was the first to offer their application method [4] based on the experimental data for cyclic sport disciplines. Weightlifting, however, is different from the basic cyclic sport disciplines in many aspects including the athletes’ anthropometrical characteristics, weight categories, totally different movement sequences and seasonality-independence of the training and competitive process. It is the heavyweight category (HWC) that is particularly specific in its anthropometrical characteristics dominated by high body weight, length and fat mass. As mentioned by A.V. Chernyak [11], for instance, fat mass in the HWC averages 28kg versus 6.6kg in the 82.5kg category, with both of the categories being widely different in many aspects including applied training weights, back squats and high- and sub-maximal weight lifts.

Some authors note that the heavyweight athletes with high body length are tested with somewhat different biomechanics of the classical snatch, clean and jerk combination with the relevant timing and strength control aspects [2, 7]. These and other considerations are particularly important for the HWC athletes whose performance is further complicated by the relatively (versus the lighter categories) lower cardiac output and higher fat-to-muscle-mass ratios – that require, among other things, longer rest breaks in the training practices.

It may be pertinent to mention in this context that lighter heavyweight athletes with relatively moderate body mass and higher active mass ratios (i.e. higher strength resources) may successfully compete with higher-weight athletes in the same weight category. It is the open high end of the HWC, in our opinion, that makes competitions in this weight class less predictable and, hence, more exciting versus the lighter weight categories.

Due to the above and other reasons, own training scope and intensity management concepts are applied in modern weightlifting sport [1, 5, 10, 7, 8, 9,]. The common and popular educational approach, for instance, applies weight lift counts (WLC) as the core criterion of the training work scope, albeit, as has been reasonably noted by V.F. Skotnikov [7], the work scope largely depends on the anthropometrical characteristics, i.e. the same WLC may have different training effects on the body with widely different anthropometrical characteristics. Therefore, reliance on WLC only is obviously one-sided, and it is only logical that training load should be rated in kilograms as was proposed by N.I. Luchkin [3] some 80 years ago.

It was found that, upon completion of the body growth process followed by the body biomechanics perfection process on the whole and the weight control biomechanics in particular, the weigh travel trajectory tends to stabilize [2]. This stabilization is normally associated with a breakthrough in the technical and competitive progress of the athletes with the HWC World Class Masters of Sport reaching 200kg in snatch and 250kg in clean and jerk. No wonder that such loads require the body capacities being fully mobilized with the athletes being inevitably exposed to training and competitive process related injuries. The above considerations force the sport community look for new, more efficient training load rating tools with the work scope being at least measurable by objective physical values.

Objective of the study was to provide grounds for and develop a new training load rating method for the modern weightlifting sport with application of energy costs valued in the International Physical Values Rating System (Systeme International d`Unitas, SI) i.e. in Joules (J) and kilo-Joules (kJ).

Methods and structure of the study. Weight travel trajectories for the classical moves in weightlifting were profiled and analyzed to compute the energy costs of the classical moves in the SI values.

Study results and discussion. In kinematic terms, any training or competitive load may be interpreted as the work geared to lift a weight to a certain point, the work being measurable by some objective physical values including mass, force, acceleration rate and travel path. Therefore, work can be calculated by the traditional formula A=Fs, with A= mgh[1]; with the work scope dependant on the weight path and mass. Thus when an athlete lifts 200kg weight 230cm high from the floor, the work is estimated at

A=m (200kg)∙g (9.8 m/с²) h (2.30m) = 4508J (4.5kJ) (1)

A weight travel path, however, is never linear nor perfectly vertical, particularly in the tear-off phase, so the relevant adjustments need to be made to the above calculations. In the tear-off phase, the weight travel path may be drawn by two arches fairly close to the body lines i.e. 6cm far from the body in the lower trunk area and 2cm in the chest area: see Figure 1. This is the reason for the weight to travel extra 4cm, with the energy cost of the extra path estimated at 78 J or roughly 0.1 kJ as follows:

A=m (200kg)∙g (9.8 m/с²) h (2.34m) = 4586 J (4.6 kJ) (2)

Furthermore, it may be beneficial to somewhat simplify the calculations by the acceleration rate being rounded up from 9.8 m/с² to 10.0 m/с², with the above formula transformed to:

A=m (200kg)∙g (10.0 m/с²) h (2.3m) = 4600 J (4.6 kJ) (3)

This adjustment offsets the previous adjustment (2) and gives quite a reasonable approximation for the work scope that may be calculated as the weight multiplied by the path by the acceleration rate of 10.0 m/с² as indicated by the latter formula (3).

Comparative analysis of the energy costs for elite weightlifters in different weight categories demonstrates benefits of this method for the training systems applied in the sport: see Table 1.

Table 1. Comparative energy costs of the two-hand clean and jerk in two weight categories

As seen from Table 1, the energy costs are widely different for the lightweight (Osmonaliev Kanybek) versus heavyweight athletes due to the weight fixing height and mass. These considerations need to be factored in the training system design and management process at every stage. It should be noted, however, that the real energy costs may be higher than those provided in the first approximation. Let us consider the key elements of the weight travel path in case of the 264kg clean and jerk (the competitive result of A. Lovchev in the 2015 World Championship in Houston) proceeding from the following assumptions:Clean and jerk is the combination of two moves, and its weight travel path may be broken down into five elements including three upward move phases (tear-off, standup from a semi-squat and clean; and two downward move phases (squated stand-up and semi-squat). The weight travel path (s) is measured from the mass centre on the bar 22.5cm (roughly 22cm) from the floor. The weight travel path (s) is always longer than the weight lifting height (h) albeit the weightlifting work is independent of the trajectory conditional on the weight movement pace being even along the path.

Upon the weight tear-off and acceleration phase, its further movement is largely inertial with the growing kinematic energy, with the athlete acting in this phase on the weight indirectly, virtually with no muscular effort applied. Our analysis of the movement video captures showed that the tear-off phase may be considered completed when the weight is 131cm high (and the weight travel path is 109cm): see Figure 1.

In the first downward movement phase, in transition to the semi-squatted position, the weight movement is partially reversed with the weight lowered 46cm down and found only 85cm from the floor at the fixing moment. Since the weight is driven by gravity in this phase, the actual work equals zero according to the body movement mechanics.

In the standing from the semi-squatted position phase, the weight travels 74cm up to be fixed 159cm high (or 137cm high from the starting position) on the chest. Then the athlete executes a fast semi-squat with the weight lowered by 18cm, with the total weight travel path increased correspondingly to reach the weight fixing point. In the weight lowering process, the kinematic energy is converted into the potential energy determined by the weight bar spring and athlete’s muscle resilience that are so critical in the final phase of the movement sequence [10].

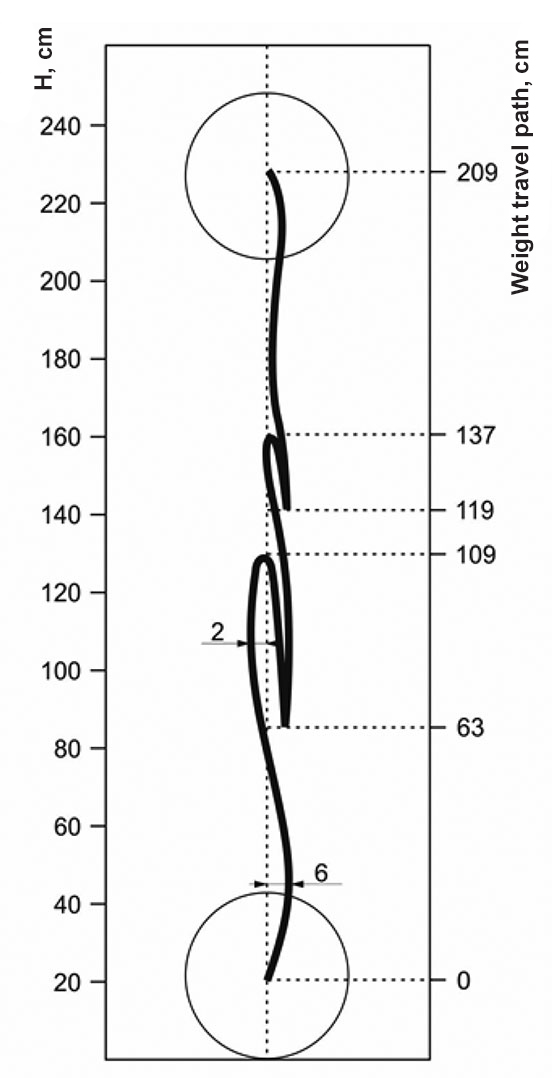
Figure 1. Weight travel path in the two-hand clean and jerk sequence

In the next phase, when the weight is pushed up from the chest, the potential energy is converted into the kinematic one again, and the higher is the latter the higher is the weight speed. The weight travel section in this phase is the longest one (84cm) to reach the top weight fixing point of 230cm. The real weight travel path may be estimated as follows: (1) Tear-off phase: +109cm; (2) Stand-up from the semi-squat phase: +74cm; and (3) Push-up from the semi-squat phase: +84cm; that gives 267cm in total. Energy cost of the above work may be estimated as follows:

A=m (264kg)∙g (10.0 m/с²) h (2.67m) = 7049 J (7.05 kJ) (4)

Therefore, in view of the fact that work in the gravity field is irrespective of the movement trajectory; and conditional on the upward movement of the weight being assumed to be linear and even; the partial and total work scope may be fairly calculated using formula A = Fs, or A = mgh. In the first case (i.e. in the first approximation) the work may be calculated as required to lift the weight straight to the fixing point; and in the second approximation, it may be calculated as the work required to move the weight by the actual travel trajectory (4). 

Conclusion. The study shows benefits of the work scope metering method with application of the energy costs valued in the International Physical Values Rating System (Systeme International d`Unitas, SI) i.e. in Joules (J) and kilo-Joules (kJ); with due account of the weight fixing point and real weight travel path in the classical snatch, clean and jerk. In contrast to the existing traditional WLC (weight lift counts) work scope metering method, the proposed new method gives reasonable and fair accounts of the real energy costs in the weightlifting sport. The new method is applicable in the training process by weightlifters of any weight category albeit may be the most beneficial for the light heavyweight and heavyweight ones. The proposed method gives sound theoretical grounds for the energy cost calculations in application to a wide variety of movement sequences in the modern weightlifting sport.

References

1. Vorobyev A.N. Tyazhelaya atletika. Uchebnik dlya institutov fizicheskoy kultury [Weightlifting. Textbook for physical culture institutes]. Moscow: Fizkultura i sport publ., 1972, 314 p.
2. Livanov O.I., Falameev A.I. O nekotorykh biomekhanicheskikh kharakteristikakh dvizheniya shtangi v ryvke i pri pod'eme na grud [Some biomechanical characteristics of barbell snatch movement and hand squat]. Tyazhelaya atletika. Ezhegodnik [Weightlifting. Annals]. Moscow: Fizkultura i sport publ., 1979, pp. 22-25.
3. Luchkin N.I. Podnimanie tyazhestey [Weight lifting]. Moscow: Fizkultura i sport publ., 1940, 196 p.
4. Matveyev L.P. Problema periodizatsii sportivnoy trenirovki [Problem of periodization of sports training]. Moscow: Fizkultura i sport publ., 1964, 244 p.
5. Medvedev A.S. Obiem i intensivnost trenirovochnykh nagruzok v sorevnovatelnom periode u silneyshikh tyazheloatletov SSSR. Avtoref. dis. kand. ped. nauk [Volume and intensity of training loads in competitive period for the strongest weightlifters of the USSR. PhD diss. abstract]. Moscow, 1968, 17 p.
6. Roman R.A., Shakirzyanov M.S. Zhim, ryvok, tolchok. Tekhnika luchshikh atletov mira [Clean and jerk. Technique of the best athletes of the world]. Moscow: Fizicheskaya kultura i sport publ., 1970, 144 p.
7. Skotnikov V.F. Partsialnye ob'emy nagruzki (s otyagoscheniem ³70%) v osnovnykh gruppakh uprazhneniy u silneyshikh tyazheloatletov mira 80-kh godov v zavisimosti ot massy tela i tipa podgotovki. Dis. kand. ped. nauk [Partial load volumes (with ≥70% weight) in main exercise groups for the strongest weightlifters of the world in the 80s, depending on body weight and training type. PhD diss.]. Moscow: Fizkultura i sport publ., 1 976, pp. 19-24.
8. Smirnov V.E. Raspredelenie nagruzki po zonam intensivnosti v osnovnykh gruppakh uprazhneniy u silneyshikh tyazheloatletov mira 80-kh godov v zavisimosti ot massy tela i etapa podgotovki. Dis. kand. ped. nauk [Load distribution by intensity zones in main groups of exercises for the strongest weightlifters of the world in the 80s according to body weight and training stage. PhD diss.]. Moscow, 1996, 180 p.
9. Solonenko O.A. Osobennosti raspredeleniya trenirovochnoy nagruzki u zhenschin tyazheloatletok vysshey kvalifikatsii. Dis. kand. ped. nauk [Specifics of training load distribution in elite female weightlifters. PhD diss.]. Moscow, 2004, 144 p.
10. Frolov V.I., Levshunov N.P. Fazovaya struktura tolchka shtangi ot grudi [Phase structure of clean and jerk]. Tyazhelaya atletika. Ezhegodnik [Weightlifting. Annals], Moscow: Fizkultura i sport publ., 1979, pp. 25-28.
11. Chernyak A.V., Chuzhin A.V., Gisin M.S. et al. Obiem i intensivnost trenirovochnykh nagruzok atletov razlichnykh vesovykh kategoriy [Volume and intensity of training loads for athletes of different weight categories]. Weightlifting. Yearbook.

Corresponding author: Fizkult@teoriya.ru

Abstract

Objective of the study was to provide grounds for and develop a new training load rating method for weightlifting sport with application of energy costs in the International Physical Values Rating System (Systeme International d`Unitas, SI) i.e. in Joules (J) and kilo-Joules kJ.

Weight travel trajectories for the classical moves in weightlifting were profiled and analyzed to compute the energy costs of the classical moves in the SI values. The new method gives objective and adequate data on the energy costs of the weightlifting moves that may be applied to control the training process in different body weight categories, with a special emphasis on the heavyweight group. The new method may be beneficial for the energy cost profiling for different movement sequences in the modern weightlifting sport.