Dr.Hab., Professor  V.I. Zagrevskiy^{1, 3}
Dr.Hab., Professor O.I. Zagrevskiy^{2, 3
1}Mogilev State University named after A.A. Kuleshov, Mogilev, Belarus
²Tyumen State University, Tyumen
³National Research Tomsk State University, Tomsk

Keywords: sport exercise, control, trajectory, motor skill, biomechanical system.

Background. Motor skills are often executed with kinematic deviations from the ideal programmed trajectory [3, 4] that may be referred as the sample technique execution sequence. Execution versions of standard technical actions varied in the amplitudes, timing and speed may facilitate technical progress or be erroneous in some aspects. Technical errors in execution may be defined as the ‘… parametric deviation of a motor skill from its ideal program’ [2, p. 688], with a technical error being qualified also in comparison with such ideal movement program/ model. Therefore, a sport-specific motor skill may be governed by a reference kinematic model of joints flexion-extension movements having a certain goal [3].

Objective of the study was to develop an adaptive control model to drive the movement sequence from the startup phase state to the required final state.

Method of the study. We used movement biomechanics methods for the movement structure analysis and biomechanical structuring of exercises; automatic control methods to synthesize the adaptive control mechanism with a feedback capacity; and modeling methods to mimic a movement sequence on a computer.

Results and discussion. We may assign certain phase coordinates for the startup, interim and final phases of any movement sequence [1]. Let us define the controlled subject by: S₀ – startup coordinate, V₀ – startup speed, S_k – final coordinate, and V_k – final speed. Now let us consider the case (guide task [1]) when the subject should be guided for time T_k to the final point with S_k coordinates from the startup point with S₀, V₀ coordinates.

Programmed control (u) may be described by the following function:

.                                                   (1)

u – control function from the class of polynomials, t is time, - second derivative from S coordinate by time.

If the final speed V_k is unlimited by some conditions, the control function u includes the following unknown parameter

.                                                                       (2)

As provided by study [1], S_k coordinate in the final time moment T_k equals:

                                   .                                                     (3)

Based on (3) let us now define the control function (u) and the free parameter (C₀):

,           .                                   (4)

Adaptive control may be designed on a feedback basis, i.e. the current condition of the subject at any time t is considered the startup point. Based on [1] we get:

.                                 (5)

T_k – required time point;  – remaining movement time; and S, V – is the coordinate and speed at the time point t. It should be noted that when the final time is , the computer will stop. As provided by [1], a division on 0 may be prevented as follows:

.                                              (6)

Coefficients (k) in the above equation are produced by the following formulae:

;     ; ;                        ;               .                (7)

Note that ∆T – is the management rigidity varying within 10-25% of T_k.

Computation experiments were run in the study using a VisualBasic 2010 Express based computer software of our own design, with the software system efficiency being rated by a control mission synthesizing case with a feedback capacity. Let us consider the products of the computation experiments on the following two cases: see Figures 1 and 2.

Input data for the Computation experiment 1: programmed control S₀=0; V₀=20, S_k=400; adaptive control S₀=0; V₀=10, S_k=400. Time parameters: T_k=20, ∆T =3.

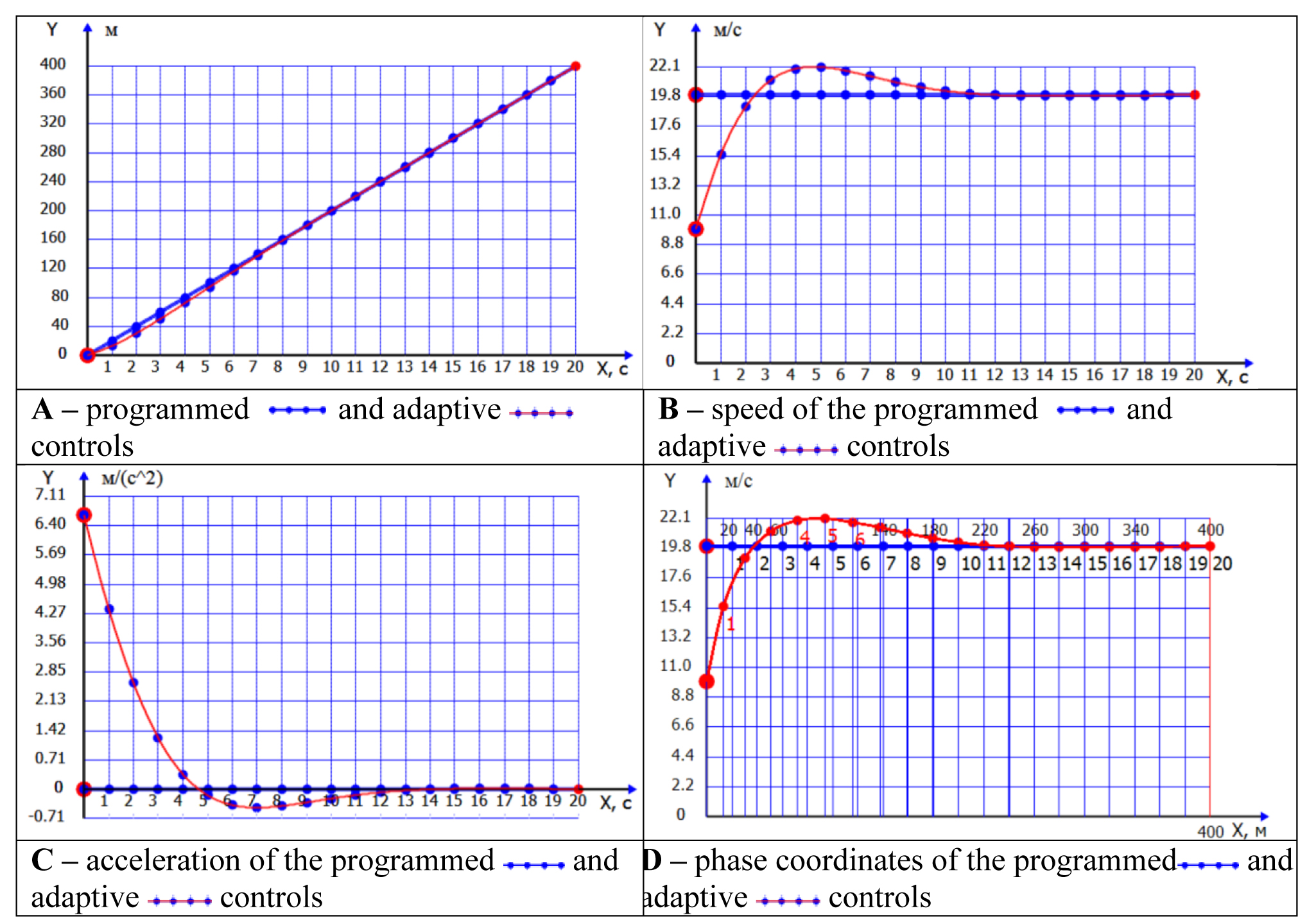
Figure 1. Computation experiment 1

Input data for the Computation experiment 2: programmed control S₀=0; V₀=20, S_k=400; adaptive control S₀=-10; V₀=-10, S_k=400. Time parameters: T_k=20, ∆T =3.

Computation product: coefficients in the control algorithms (in the both computation experiments) are the following:

.Control trajectory (coordinates, speed, acceleration) and phase coordinates are given hereunder on Figure 2.

It should be mentioned that the input data for the adaptive control at the startup time moment in Computation experiment 2 changed albeit the control logic (5) remained the same as in Computation experiment 1.

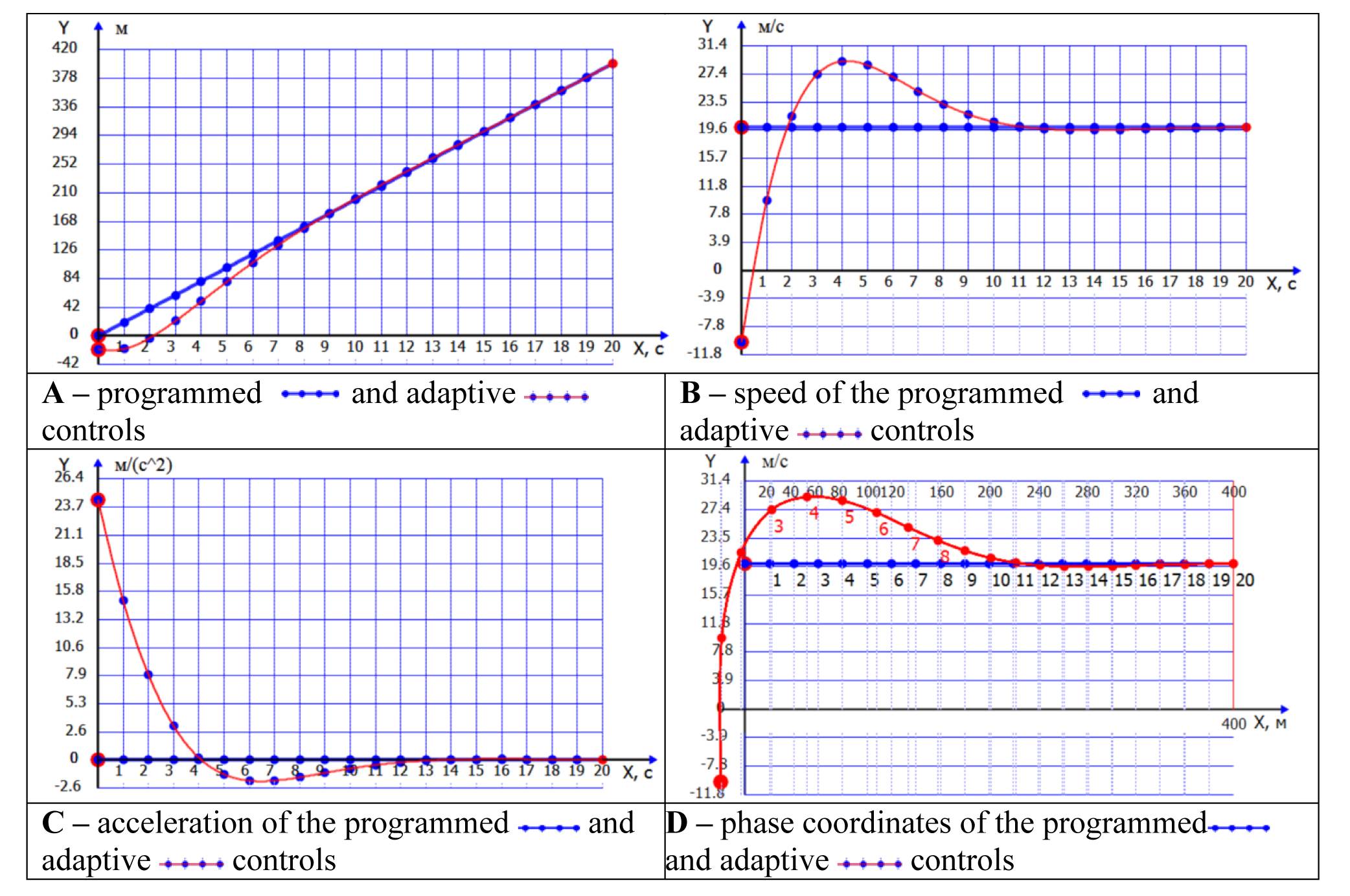
Figure 2. Computation experiment 1

Conclusion. The guiding logic synthesized by the computation experiment to solve the guide task was formed in an automatic mode for computations in the programmed control and adaptive control scenarios. The qualitative values of coefficients in the control equations are influenced by the startup coordinates and speeds for the startup (S₀, V₀) and final (S_k) moments of time; plus the modeling process time (T_k) and preset rigidity of the control process (∆T).

The control logic is not affected by changes in the adaptive control conditions, with the changes only forming a new adaptive control model accommodated to the changed conditions, movement trajectory and programmed control parameters to attain the goal of the movement sequence at the final time point. This finding of the study makes it possible to qualify a movement error as the result of a kinematic disorder in the real movement versus the programmed model. In this case the adaptive control will compensate the movement error and put the subject back on the programmed trajectory.

References

1. Batenko A.P. Control of final state of moving objects. M.: «Sov. radio» publ., 1977. 250 p.
2. Gaverdovskiy Yu.K. Teaching sports exercises. Biomechanics. Methodology. Didactics. M.: Fizkultura i sport publ., 2007. 912 p.
3. Zagrevskiy V.I., Zagrevskiy O.I. Technical mastery rating in sports by biomechanical movement indices. Teoriya i praktika fiz. kultury. 2018. no. 10. pp. 76–78.
4. Sosunovskiy V.S., Zagrevskaya A.I. Kinesiological potential of senior schoolchildren. Teoriya i praktika fiz. kultury. 2018. no.10. pp. 62–64.

Corresponding author: zvi@tut.by

Abstract

Motor skills are often executed with kinematic deviations from the ideal programmed trajectory that may be referred as the sample technique execution sequence. The article considers a mechanical-mathematic control model to compensate errors in the startup coordinates and secure a right body positioning on the programmed trajectory. Objective of the study was to develop an adaptive control model to drive the movement sequence from the startup phase state to the required final state. We used movement biomechanics methods for the movement structure analysis and biomechanical structuring of exercises; automatic control methods to synthesize the adaptive control mechanism with a feedback capacity; and modeling methods to mimic a movement sequence on a computer. Subject to the study was the adaptive control to secure the movement sequence being guided from the startup phase to the required final phase. The goal was achieved by a computer model of the movement produced by targeted computation experiments. The article overviews the adaptive control building mathematical toolkit and findings of the computation experiments. The study has resulted in the new motor errors compensating adaptive control model designed to guide the controlled subject into the required final phase.