Biomechanical Characteristics of Motion: Where and How You Can Use "Gradient Force"?
Фотографии:
ˑ:
B.A. Dyshko, Ph.D., Dr.Biol.
Sport Technology LLC, Moscow, Russia
Assessment of the level of development of speed and strength qualities and abilities is one of the major tasks of sports pedagogics. Naturally, such an assessment is carried out both when doing certain exercises performed under standard conditions, in the standard motor program and using the metrologically tested equipment of the same type and when doing competitive and/ or simulation exercises using specific characteristics. It is desirable that these characteristics would have a physical and/ or biomechanical sense and describe the studied qualities and abilities [1 - 4, 8].
At the same time, when assessing examined skills and abilities a scientist/ a trainer can enter/ use his own characteristics, giving a detailed definition of the used term.
The term "gradient force" is used as a characteristic describing "explosive effort" [1, 2, 5, 6, 8]. According to the definition, when performing movements with maximum "explosive efforts" an athlete should develop greater strength within the shortest period of time.
Mathematically, by definition, "force gradient" is equal to the first derivative of force with respect to time [1, 2, 5, 8]
gradF = dF/dt (1)
where: gradF, n/s – the value of “gradient force”,
F, n – estimated force,
t, - force action time.
The diagram of "explosive effort" applied to a dynamometer is shown in Figure 1.
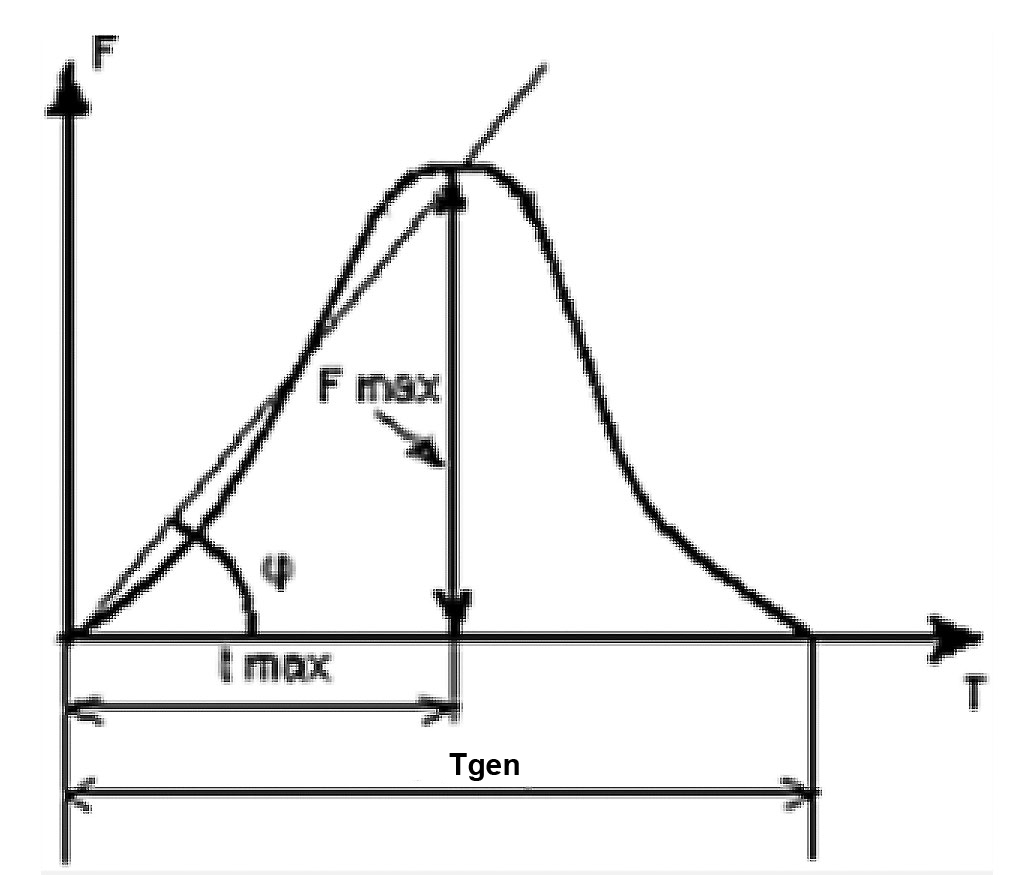
Figure 1. The force build-up curve at a single "explosive" effort followed by immediate relaxation [1, 2, 8]. Legend in the text.
In practice, the "gradient force" is quantitatively described using the following parameters: time to force equal to half maximum force Fmax, equal to tmax/2, time to maximum force tmax, speed- strength index I = Fmax/tmax [1, 2, 5, 8]. Often the speed strength index I is also called "gradient force".
Note that all the above applies to unidirectional movements.
For strength diagram (Figure 1), under certain assumptions (strength increases and "reduces" linearly) the average power N of force F, applied to mass M, within Tgen will be equal to
N = [tmax2 • Tgen • (gradF)2]/ 2•M= (2)
Proceeding from the formula 2, the higher the speed-strength index I or "force gradient” gradF is, the higher the average power N is for the time of application of force F to an apparatus with the mass M.
That is, in general, the speed-strength index I or "force gradient” gradF reflects the power being developed with this force.
Yu.V. Verkhoshansky [1] suggested using the characteristic, which he called the "reactivity coefficient" RC for motions that move own body
RC= Fmax/(tmax •M)= I/M= (gradF)/M (3)
Let us remind that "explosive force" is a characteristic that describes athlete's ability to develop a significant force within the minimum amount of time in unidirectional movements.
Let us consider two jumping motions used to test athletes’ speed and strength abilities: vertical jump from a static posture and vertical jump "with a squat".
Dynamograms of the vertical component of reaction force when these jumps are shown in Figures 2, 3, 4.
Jumps were performed on a dynamometric platform, designed and produced in Russia, the company "MBN". The natural frequency of the platform is at least 500 Hz, the relative error of measurement is less than 2%. The signal from the platform is processed using a specially designed program [3]. The "common center of mass (CCM)" travel dynamics during an exercise can be displayed along with the curve of the vertical component reaction force.
The dynamogram of the vertical component of support reaction force (VCSRF) synchronously with the path of movement of the common center of mass (CCMB) of the body of an athlete during the exercise "Vertical jump from static posture" is adduced in Figure 2. The figure shows that the movement is unidirectional. That is, the speed-strength index of VCSRF or reactivity coefficient is significant in this case.
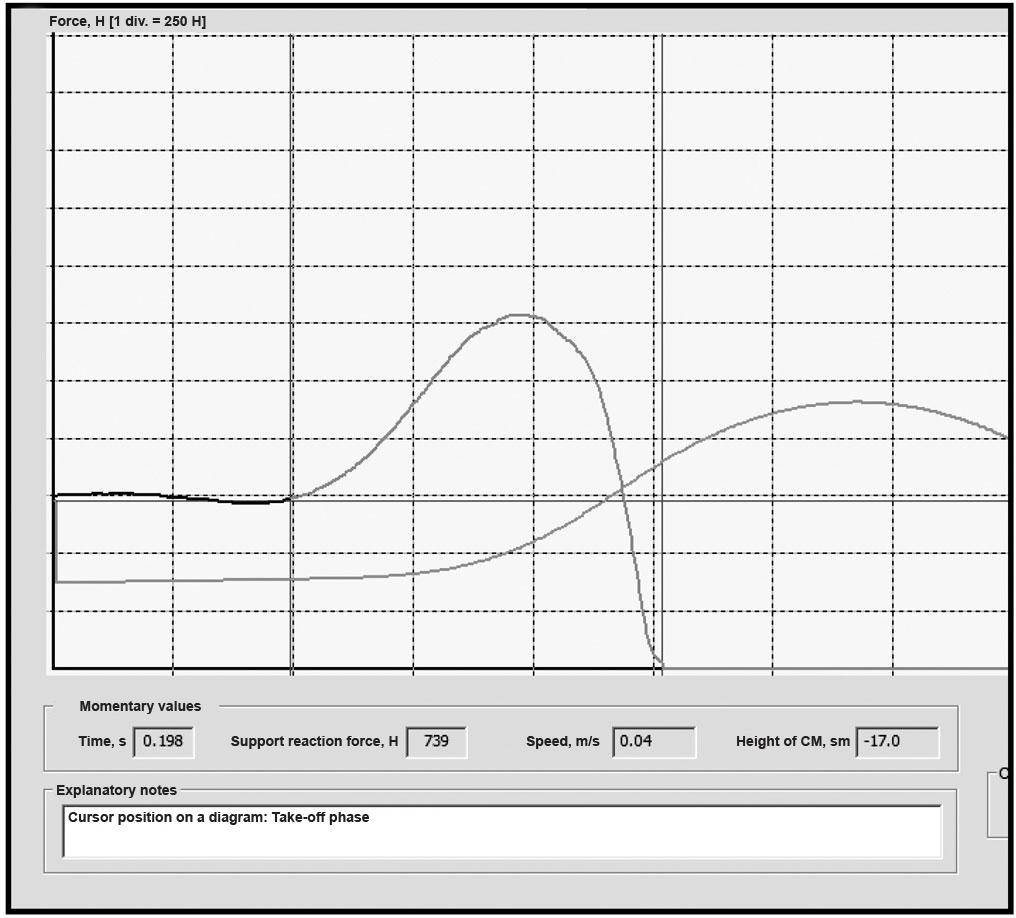
Figure 2. The dynamogram of the vertical component of support reaction force during the test “Vertical jump from static posture without arm swing”. Legend in the text.
Cursor position on a diagram: Take-off phase
In biomechanics [2, 3, 8] support reaction force to the take-off movement Ft.m. is used to describe the external forces used on the CCMB when pushing, along with the support reaction force. The vertical component of this force Fzt.m. is equal to
Fzt.m. = F(t) - mЧg
As Figure 2 shows, the value of force Fmax is used to detect the speed-strength index I or the gradient force or the reactivity coefficient is the maximum value of the vertical component of support reaction force to the support reaction force to the take-off movement. It is to be stressed once again that the use of the reactivity coefficient is appropriate only for unidirectional movements.
Now we are to consider the dynamogram of VCSRF, obtained in the exercise "Standing vertical jump with a squat". In this case, we have two calculation procedures of the speed-strength index.
Figure 3 shows the dynamogram of VCSRF of a vertical jump with a squat and the calculation procedure of the reactivity coefficient from the book by V.L. Utkin "Biomechanics of physical exercises", Moscow, 1989 [8].
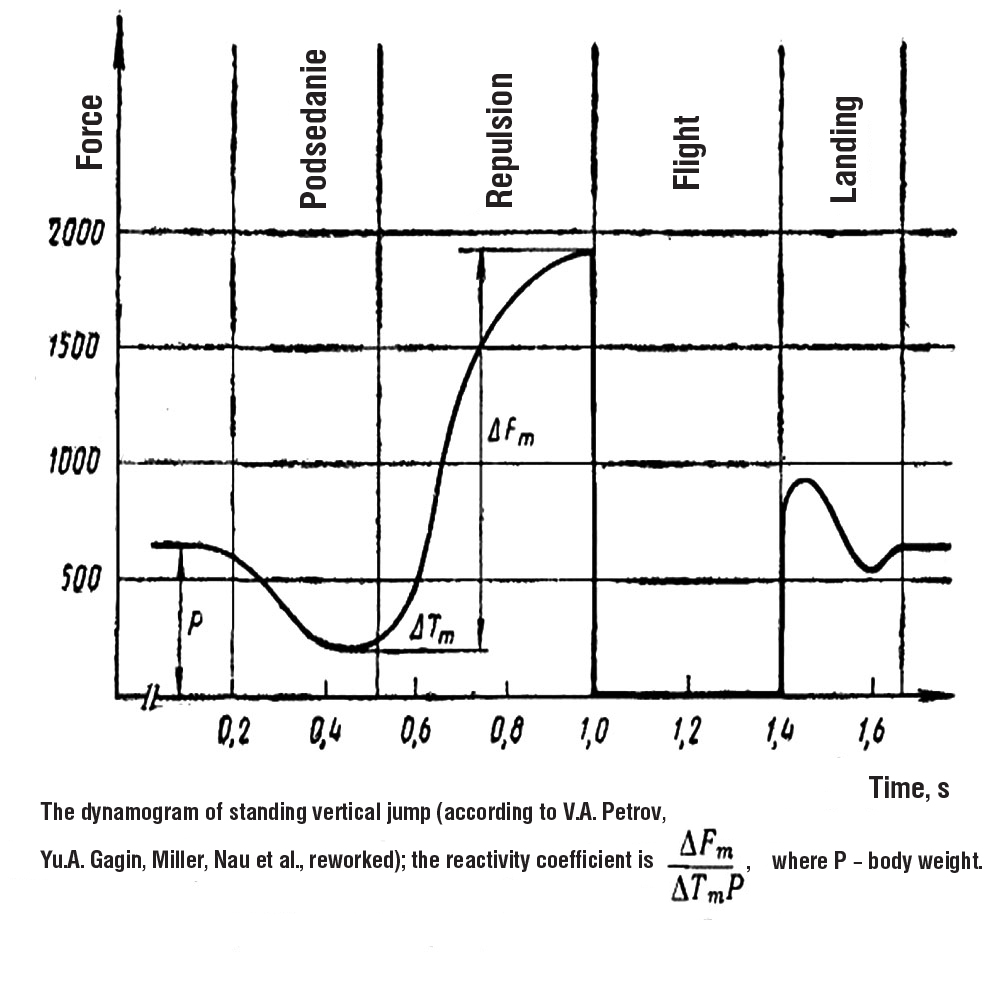Figure 3. The dynamogram of VCSRF of vertical jump with a squat and the calculation procedure of the reactivity coefficient from the book by V.L. Utkin "Biomechanics of physical exercises", Moscow, 1989.
Fig. 31. The dynamogram of standing vertical jump (according to V.A. Petrov, Yu.A. Gagin, Miller, Nau et al., reworked); the reactivity coefficient is …, where P – body weight.
Despite the fact that the dynamogram of VCSRF is divided into phases - squat, take-off, fly, landing - to calculate the reactivity coefficient the value of Fmax is measured from the lowest point of the dynamogram of VCSRF (Fig. 3), although at this time CCMB still goes down – no take-off yet. Is this method legitimate or not?
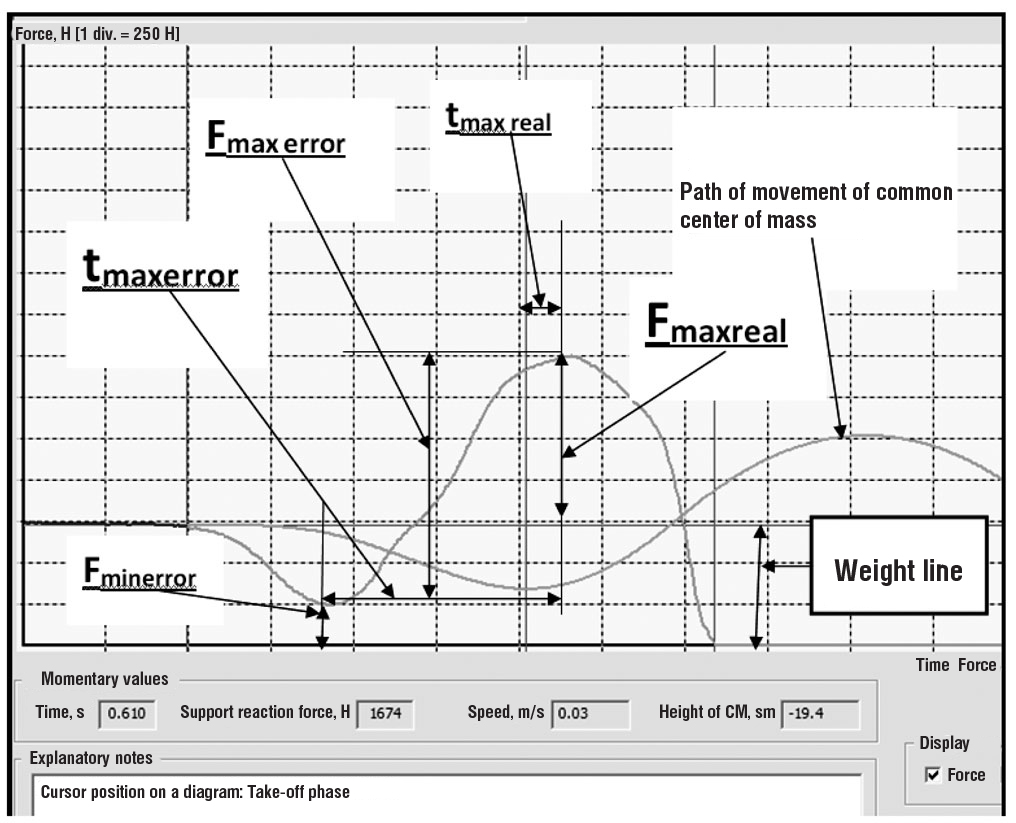
Figure 4. Dynamogram of the vertical component of support reaction force during the test “Vertical jump “with a squat” without arm swing”. Legend in the text.
The purpose of the work was to specify the conditions of using the gradient force or speed-strength index and biomechanically justify the calculation procedure of the speed-strength index.
Methodology. One male subject, weight (fit) 75 kg, height 179 cm was involved in the study. The subject did two exercises - "Standing vertical jump without squat" and "Standing vertical jump with a squat". Both of the exercises were performed without arm swing (arms on waist). Exercises were performed on a dynamometric platform produced in Russia, the company "MBN". The path of movement of CCMB when performing an exercise was presented on the display along with the curve of the vertical component of support reaction force. Each exercise was performed 7 times. The mean values of reactivity coefficient and standard deviations were calculated. When performing the exercise "Standing vertical jump with a squat" the reactivity coefficient was calculated using different techniques:
- “incorrect” (Fmax error and tmax error are calculated from the lower point of the dynamogram of VCSRF Fmin error);
- “correct” technique (Fmax real and tmax real are calculated from the lower point of the path of movement of CCMB, corresponding to the zero speed of movement of CCMB or start of take-off). The results of the experiment are adduced in Table 1.
Table. The values of the reactivity coefficient according to Yu.V. Verkhoshansky for standing vertical jumps with and without squat
|
N |
Standing vertical jump without squat |
Standing vertical jump with squat |
|
|
“correct” technique |
“incorrect” technique |
||
|
RC |
59,1 ± 4,9 |
266,7 ± 23,5 |
66,7 ± 5,8 |
Results and discussion.
The analysis of the dynamogram of VCSRF and the path of movement of CCMB during a standing vertical jump (Fig. 4), obtained in our studies indicates that the lowest point of the dynamogram of VCSRF does not correspond to the lowest point of the path of movement of CCMB, is not the point of "change in the direction of movement of CCMB".
It should be noted that the value of RC for the exercise "Standing vertical jump with a squat", calculated using the correct procedure is significantly higher than the one calculated using the "incorrect" procedure, despite the fact that the values of Fmax in the latter case are much higher.
Table shows that for this subject the reactivity coefficient in a vertical jump without a squat, i.e. from the static posture, is significantly lower (P < 0.05) than the "correct" reactivity coefficient in a vertical jump with a squat. This phenomenon indirectly indicates a bigger power, developed by musculotendinous structures of the lower limbs in the take-off phase, including using the elastic energy of prestressed musculotendinous structures of the lower limbs accumulated in the squat phase [4, 5].
CONCLUSIONS.
1. The characteristics of "explosive" force in various movements (gradient, speed-strength index, reactivity coefficient) are equal only to unidirectional movements.
2. For the movements associated with the movement of human/ athlete’s body the phase of movement, for which the reactivity coefficient is determined, starts from the moment of zero speed of the common center of mass.
3. The reactivity coefficient in jumping movements, that use in the take-off phase the effect of the implementation of elastic energy of musculotendinous structures, accumulated in the slowdown phase, is significantly higher than for the movements performed from the static posture.
References
- Verkhoshansky Yu.V. Fundamentals of special strength training in sport. – Moscow: Fizkul'tura i sport, 1977. – 215 P. (In Russian)
- Donskoy, D.D., Zatsiorsky, V.M. Biomechanics: Textbook for institutes of physical culture. - Moscow: Fizkul'tura i sport, 1979. – 264 P. (In Russian)
- Dyshko B.A. Modern biomechanical measurement procedures: computerized dynamometric complex // Teoriya i praktika fizicheskoy kultury. - 2000. - N 7. - P. 24-26. (In Russian)
- Dyshko B.A. Innovative technology of assessment of regenerative properties of musculotendinous structures of human lower limbs // Status and prospects of technical support of sports activity / Proceedings of the III International Scientific and Technical Conference. - Minsk, 2014. – P. 49 – 57. (In Russian)
- Zatsiorsky, V.M., Aleshinsky, I.S., Yakunin, N.A. Biomechanical bases of endurance. – Moscow: Fizkul'tura i sport, 1982. – 206 P. (In Russian)
- Zatsiorsky, V.M. Athlete’s physical qualities (the basic theory and methodology of education) / V.M. Zatsiorsky. – Moscow: Fizkul'tura i sport, 1970. – 200 P. (In Russian)
- Mitreykin, V.G. On the topography of explosive force in athletes / V.G. Mitreykin, V.D. Andris / / Improvement and management of the training process. - Tashkent, 1981. – P. 20-22. (In Russian)
- Utkin, V.A. Biomechanics of physical exercises: Study guide for departments of physical education. – Moscow: Prosveschenie, 1989. – 205 P. (In Russian)
